求一个向量在另一个向量上的投影

对于任一向量 $\vec a$ ，计算在向量 $\vec b$ 上的投影，可以把向量 $\vec a$ 分解为 $\vec a_{\shortparallel}$ 和 $\vec a_{\perp}$ , 有 $\vec a = \vec a_{\shortparallel} + \vec a_{\perp}$ , 其中$\vec a_{\shortparallel}$ 是平行于$\vec b$ 的， $\vec a_{\perp}$ 是垂直与$\vec b$ 的。

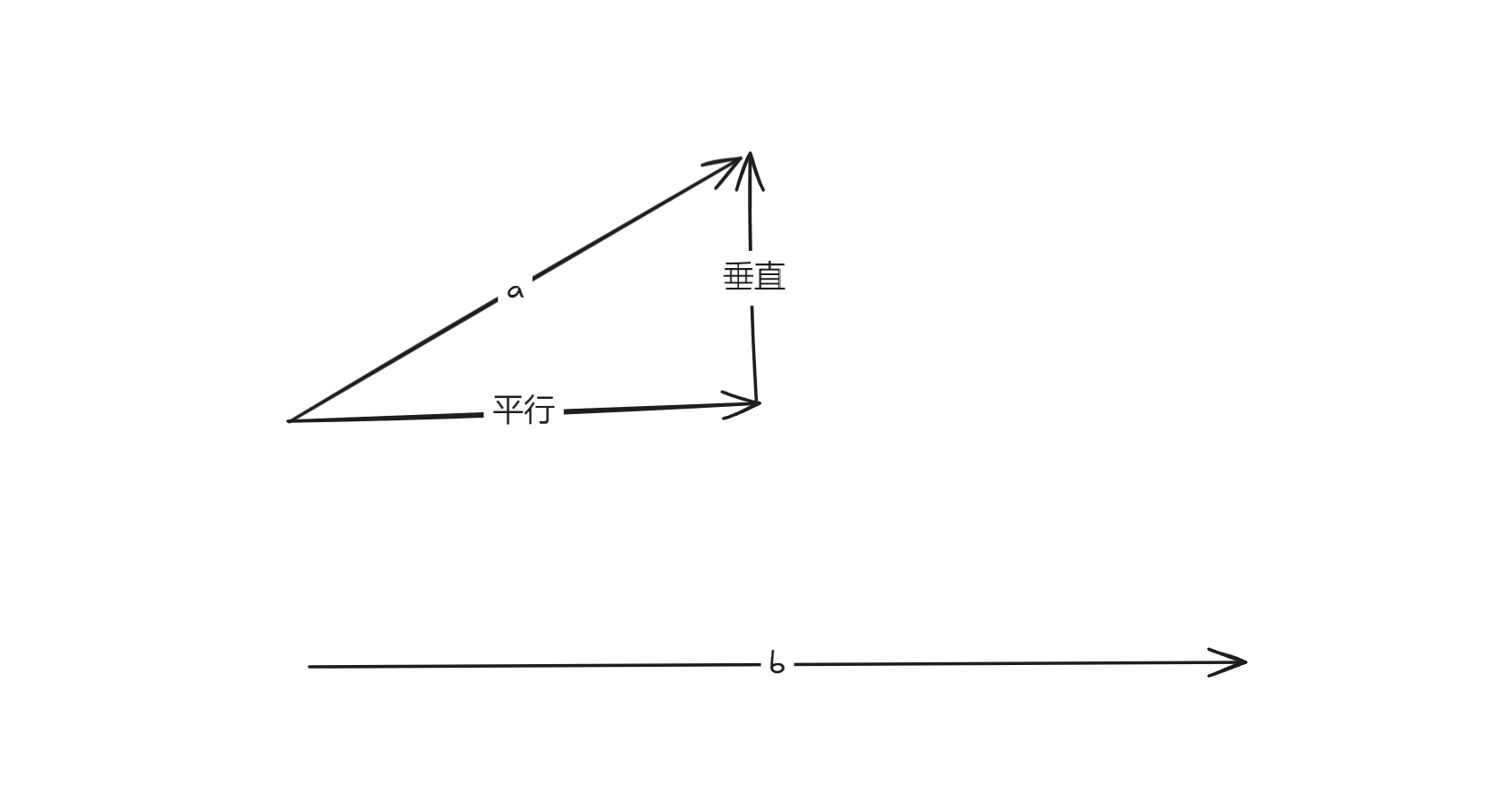
如图，求向量 a 投影到向量 b 的投影，只需要求平行于 b 向量的长度即可。

然后可以观察到，a 平行 是平行与 b 向量的，所以容易得到，$\vec a_{\shortparallel} = \vec b\frac{\left|\vec a_{\shortparallel}\right|}{\left| \vec b\right|}$

然后观察到 $\cos \theta = \frac{\left|\vec a_{\shortparallel}\right|} {\left| \vec a \right|}$

所以 $\left|\vec a_{\shortparallel}\right| = \cos \theta \left|\vec a\right|$

带入得： $\vec a_{\shortparallel} = \vec b \frac{\left|\vec a\right|\cos\theta }{\left|\vec b\right|}$

又因为向量点积的公式是： $\vec a \cdot \vec b = {\left|\vec a\right|} {\left|\vec b\right| }\cos\theta$

所以上面可以再简化为：$\vec a_{\shortparallel} = \vec b \frac{\vec a \cdot \vec b}{\left|\vec b\right|^2}$

一般如果$\vec b$是单位向量，就可以简化：

$${\vec{a}}_{\parallel }=\vec{b}\cdot \vec{a}\cdot \vec{b}$$
\vec a_{\shortparallel} = \vec b \cdot \vec a \cdot \vec b

最后再求$\left|\vec a_{\shortparallel}\right|$ 即可。